SplineComponent は３次関数でベクトルで微分で
- はじめに
- SplineComponent と『時間』について
- セグメントについて
- セグメントの数式
- その式は一体どこから来るのか
- 制御点との関係およびセグメントの連結
- 接ベクトル（Tangent）について
- 媒介変数 t と SplineComponent における時間との関係
- SplineComponent から SplineMesh へ
- セグメントの分割
- おわりに
はじめに
とりあえず公式ドキュメント
お手軽に曲線を得る手段としてみんな大好き SplineComponent について少し掘り下げる記事です。
既に使用している方はご存じかと思いますが、おおざっぱな性質として
「制御点を通して滑らかな曲線が作れる」
あるいはもう少し踏み込んで
「『時間』に対して滑らかに変化する座標やら姿勢やらが出力される」
というものであって、通常の操作においてはこのくらいの認識でも大丈夫だったりはします。
ただ、少し凝った操作をしようとして「予想した挙動と違う」「期待する結果が得られない」といった事態に直面した時、中身についてある程度把握していると問題の解決に役立つこともあるでしょう。
内容について：
- SplineComponent についての基本的な説明は含みません。
- ある程度数学的な話を含みます。
ベクトルと微分が分かるとフルに消化できるかと思います。 - SplineComponent からは座標の他に 回転/スケール を得ることができますが、
これらは設定と計算の内容が異なるのでここでは扱いません。 - なるべく基本的なところから順に書きましたがわりと徒然としています。
ご容赦いただければ幸いです。
よければ冒頭の目次を活用してください。
SplineComponent と『時間』について
先ほど「『時間』に対して～」と書きましたが、曲線は時間と特別な関係にはありません。
図形としての曲線は全体が同時に存在していますし、時間以外のパラメータをもって曲線上の点をサンプリングしても良いわけです。
ただ、時間経過によって点が移動するという状況が人間にとって比較的イメージしやすいので便宜上時間として言い表しているのかもしれません（関数・変数の名前としても Time とか Duration とかの語が使用されています）。
仮に時間としているけれど別のものと見なしても良い、ということを知っておけばここはOKでしょう。
SplineComponent にはそんな時間を扱う変数・関数が幾つかあります。
曲線に沿って何かを動かすような処理においてよく使用することになるので、触れたことのある方も多いでしょう。
- Duration : 曲線全体の始点から終点までの時間を表す変数（始点の時刻は０なので終点の時刻を表すとも言える）。デフォルトでは 1.0
- GetLocationAtTime() : 時間を入力して曲線上の位置を得る関数。０を入れれば始点、上記 Duration と同じ値を入れれば終点を得る。
他にもあります。詳しくは公式ドキュメントをご覧ください。
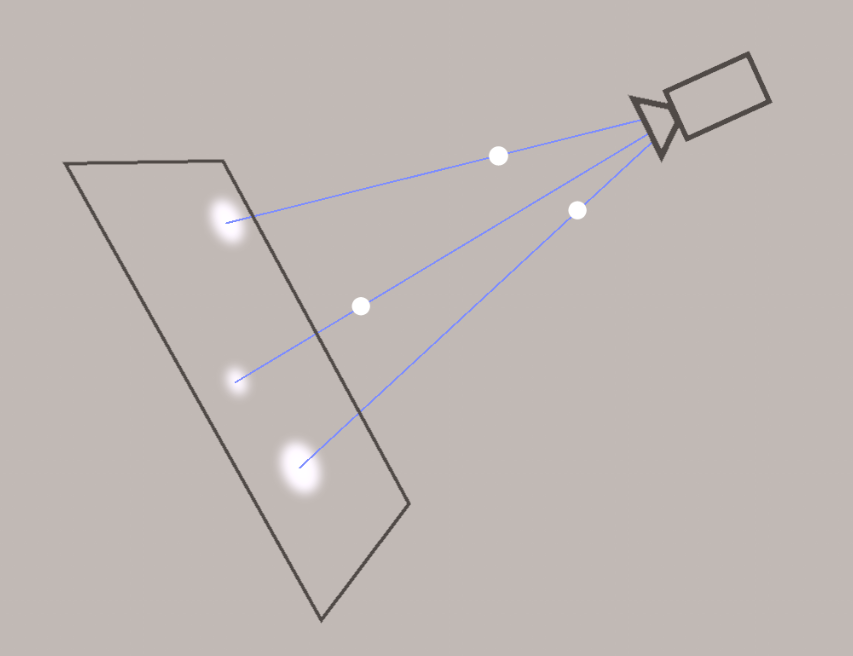
セグメントについて
SplineComponent の与える曲線は見かけ上は滑らかな一本の曲線のように振る舞い、前述したように ０～Duration の連続した時間に対して滑らかな軌跡を描きます。
しかし内部的には制御点で区切られた曲線を繋ぎ合わせたものになっています。
ClosedLoop 設定でなければ [制御点数-1] の曲線からなり、一つ一つの曲線をセグメント(Segment)と呼びます。
セグメントの数式
各セグメントは、0.0 から 1.0 を値にとる媒介変数 t についての3次関数で表現されています。
具体的には以下のような式です。
色々と記号が出てきますが、
- p(t) : カーブの値。例えば座標。
- t : 媒介変数（０～１）
- p0 : 始点（t=0）での値
- p1 : 終点（t=1）での値
- m0 : 始点（t=0）での p の変化率、あるいは接ベクトル(Tangent)
- m1 : 終点（t=1）での p の変化率、あるいは接ベクトル(Tangent)
のような意味です。
つまり p0, p1, m0, m1 がカーブを決定するパラメータであり、セグメント毎にこの組み合わせが異なるということになります。
なお、ここで t 以外はベクトルです。
その式は一体どこから来るのか
p(t) = a*t^3+b*t^2+c*t+d
のように一般的な3次式を作り、
p(0) = p0
p(1) = p1
p'(0) = m0
p'(1) = m1
を連立して a, b, c, d を求め (p0, p1, m0, m1 で表す) まとめ直すと出来上がります。
もっとスマートな導出や説明の方法があるのかもしれませんが私は知りません。
制御点との関係およびセグメントの連結
各制御点を編集するということは、それにつながるセグメント端の座標および接ベクトル（p0, m0 あるいは p1, m1）を設定するということです。
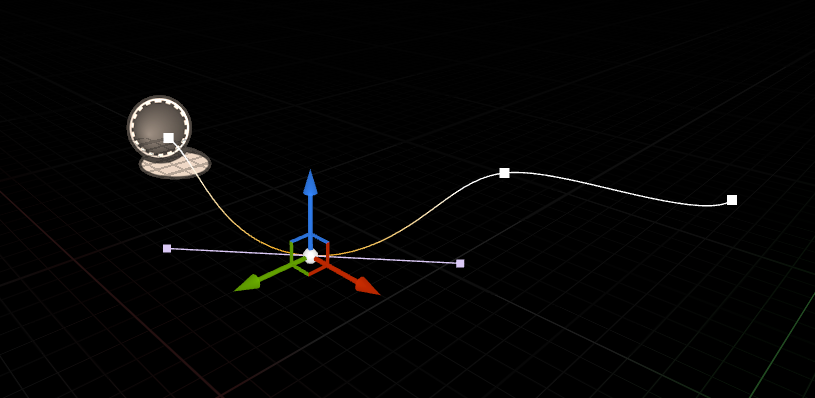
（このエディタでは中央のハンドルで座標を、両端のハンドルで接ベクトルを編集できます）
制御点は隣り合うセグメント間で共有されています。
したがって制御点から伸びる両セグメントの座標と接ベクトルが一致（※）しますので見かけ上はセグメント同士が滑らかに接続されるということになります。
※）
Segments[n].p1 = Segments[n+1].p0
Segments[n].m1 = Segments[n+1].m0
のような関係になります。
接ベクトル（Tangent）について
SplineComponent にも接ベクトル（Tangent）を取得する関数が備わっていますが、これについて少し注意が必要です。
この文脈での接ベクトルとはいわゆる接線の方向ベクトルではなく、媒介変数に対する値の変化率、ようは微分値です。
つまり
m = dp/dt
という関係です。
ベクトルの長さにも意味がありますので、接ベクトルに対して Normalize を行と必要な情報を失う場合があります。
なお、接ベクトルはやはり接線と平行です。
媒介変数 t と SplineComponent における時間との関係
セグメントの媒介変数 t と SplineComponent の時間（Time）とはわりと単純な関係にあり、互いの変化率は単に比例します。
Time から t を得る計算を疑似コードで書くと
float Key = ( Time / Duration ) * NumSegments;
int SegmentIndex = floor(Key);
float T = Key - SegmentIndex;
のような関係です。
一行目で得た Key は整数部分でセグメント番号、小数部分でセグメント内の位置を指す値ということになります。SplineComponent にはこれを扱う関数もあります（そこでは InputKey というフレーズが使用されています）。
SplineComponent から SplineMesh へ
SplineComponent と似た機能として SplineMeshComponent というものがあり、こちらはカーブに沿ってメッシュを変形させるものです。
SplineMeshComponent はセグメントを一つしか持たないので SplineComponent で作成したスプライン曲線全体を正確にカバーすることは一般にはできません。
１セグメントに対して１メッシュで満足である場合、以下の記事にあるようにセグメント数ぶんだけ SplineMeshComponent を作成することで対応できます。
セグメントの分割
セグメントを（形状を保って）統合することは一般には不可能ですが（異なる曲線であるため）、一つのセグメントをカーブの形を保ったまま分割することは可能です。
同一セグメント上から2点の座標及び接ベクトルをサンプリングし、媒介変数の変化量が１になるよう接ベクトルをスケールして出来上がりです（計算上は、少し不思議に感じるかもしれませんが接ベクトルに対して元の媒介変数の変化量を乗算することになります）。
BPでの簡単な例を載せておきます。
整数部分を同じくする StartKey, EndKey の区間でカーブを切り出して SplineMesh に設定します。
ここで StartKey, EndKey の整数部分の異なる値を設定した場合は切り出す範囲が複数のセグメントにまたがり、元のカーブに一致しない結果を得ます。
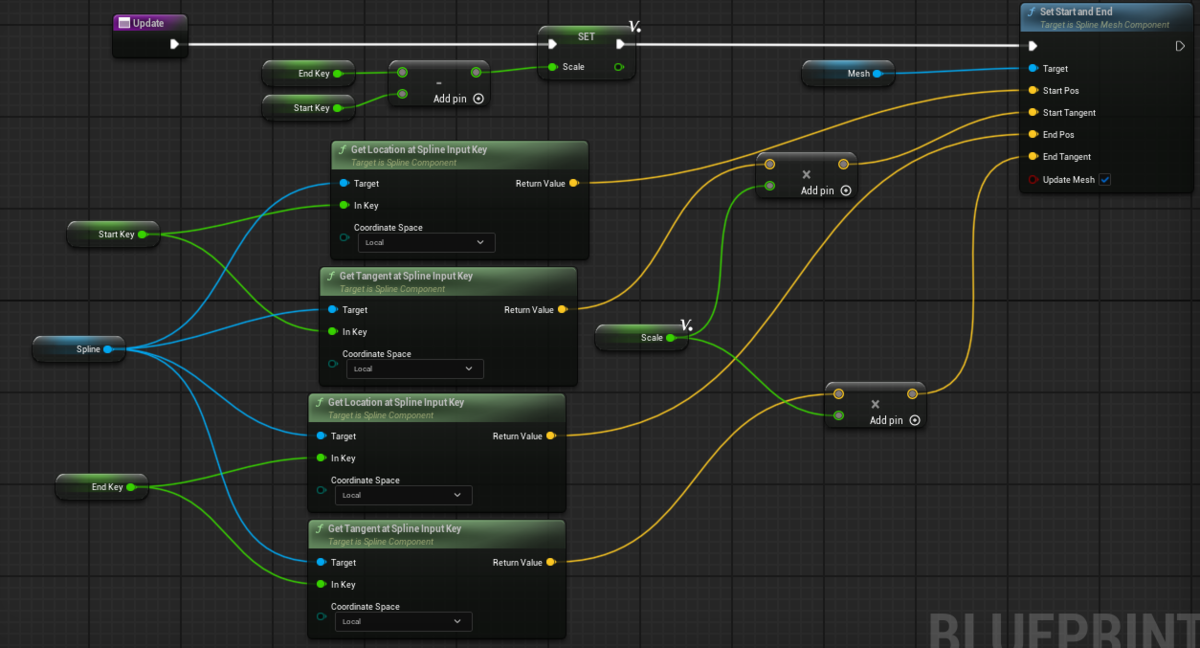
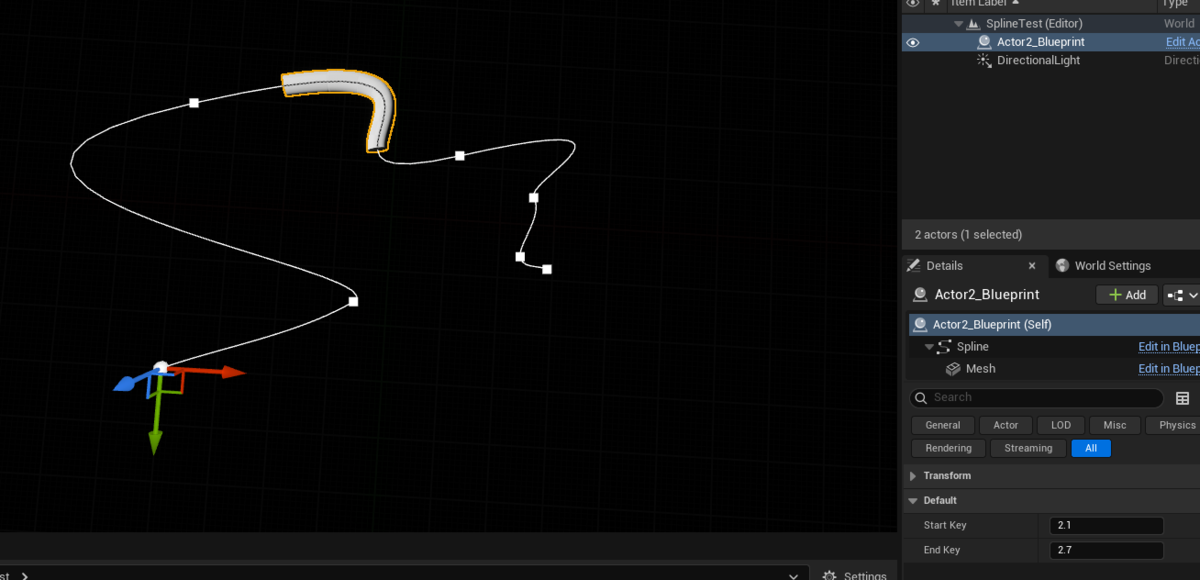
上記の例では InputKey（≒ Time）ベースで切り出し範囲を指定しましたが、カーブの長さ（カーブ上の距離）を元にして区間を切りたい場合は GetInputKeyValueAtDistanceAlongSpline 関数が便利です。
おわりに
SplineComponent の計算内容について少し掘り下げました。
このあたりを把握しておくことで Spline の加工で融通を利かせられるようになる、かもしれません。
Anime Aura VFX 技術解説③
UE5 向けの NiagaraSystem アセットである Anime Aura VFX についての技術解説です。 第１回 Anime Aura VFX の原理 前回のプロセスで生成された濃度マップを用いてオーラの外見を仕上げる処理についての説明です。 前回でオーラの濃度を2次元的に記録したテクスチャ「濃度マップ」を生成しました。 アニメで多く見られるオーラの表現ではキャラクターのシルエットとの距離に応じて濃淡や色が変化することが多いようです。 LinearColor カーブを作成します。 カーブをマテリアルから参照可能なテクスチャに変換します。 濃度マップからサンプリングした値を用いてカラー（＋透明度）を得ます。 濃度の値にノイズを乗せます。 濃度マップのサンプリング位置をワープさせることで形状をある程度操作できます。 AnimAuraVFX の最終プロセスについて説明しました。
概要 この記事について
全３回に分かれています。
第２回 パーティクルの投影
第３回 濃度マップ→表現（本記事）
基本的にはマテリアルの話になります。濃度マップについて
これは名前の通り一次元の情報ですが、マテリアルで処理して良い外見に仕上げます。カーブアトラス
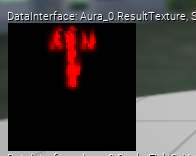
濃度マップは基本的に「中心が濃く、外側で薄くなる」ものですので直接的に表示すると上の画像のようなイメージになります（赤く表示されていますが一次元の濃淡データです）。
これをそのまま表示するのではお粗末（というか普通のエミッターを用いた方が良い）ですので、色々とマテリアルで加工していきます。
必ずしも中心付近で濃いわけではなく、外縁部を目立たせることもよくあります。
これを実現するためにカーブアトラスを用いて「濃度→カラー」のマッピングを行います。カーブの作成
・横軸が 0~1 をとるようにします。
・０が最外縁、１が中心部にあたります。
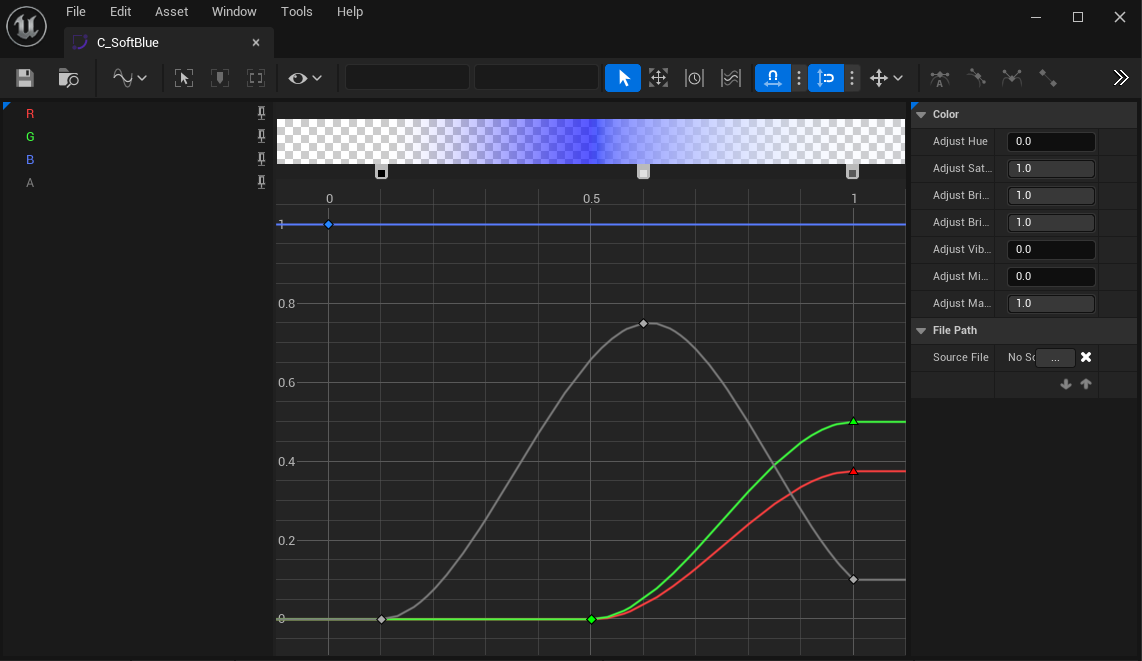
このカーブは単純なデータですがけっこう重要です。
キャラクターの体からの距離と濃度とは直線的な関係でない点に注意が必要です。実際には結果を見ながら調整することになります。
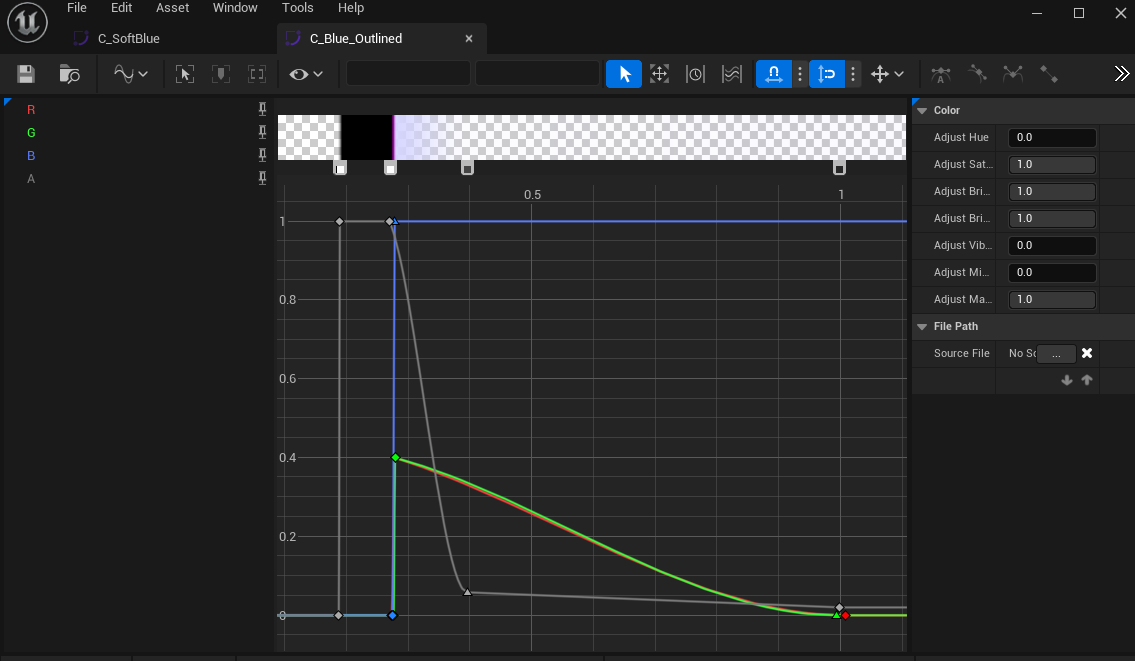
滑らかでない曲線が有効なケースもあり、外縁部分の狭い区間でいったん不透明な黒になるようにすることでアウトラインを出せたりもします
（横軸0.2～0.3あたりに着目して下さい）。
マテリアルへの取り込み
このテクスチャはカーブアトラスと呼ばれます。
節約のため高さ１のテクスチャにしています。マテリアルの作成
とにかくカラーを得られれば良いわけですが、調整のしやすさからカーブアトラスを用いるのが便利です。
最も単純な例としては以下のようになります。
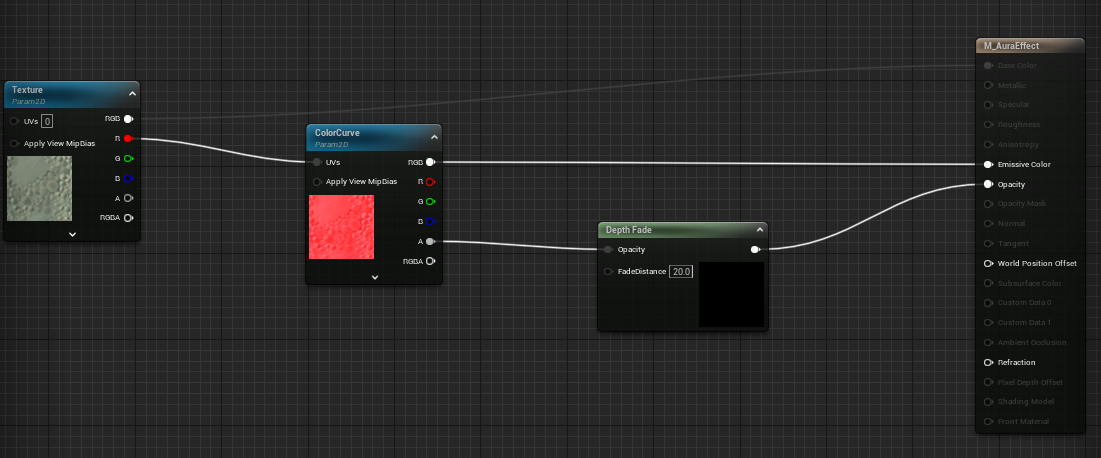
Texture = 濃度マップ
ColorCurve = カーブアトラス
これらのパラメータは NiagaraSystem から設定されます。
この段階での工夫によってもオーラの表情を変えられます。
各種マテリアル芸的なテクニックを生かせる部分です。
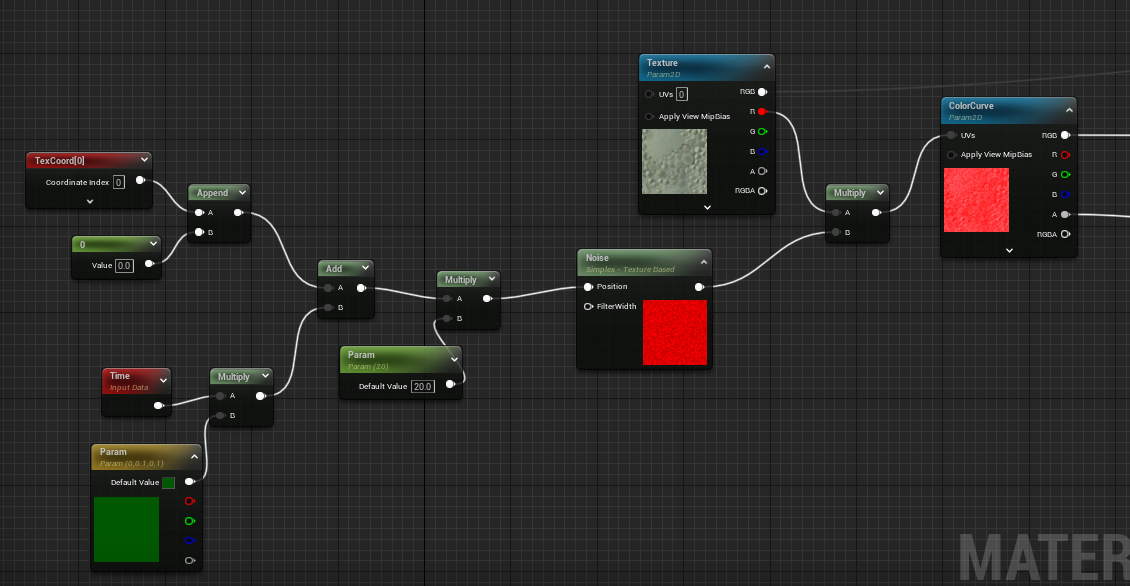
コツとしては、カラーより元となる濃度に働きかける方が概ね自然な結果を得やすいと思います。ノイズ
安直に情報量を増やすことができます。
下の例ではサンプリングされた濃度をノイズで加工しています。
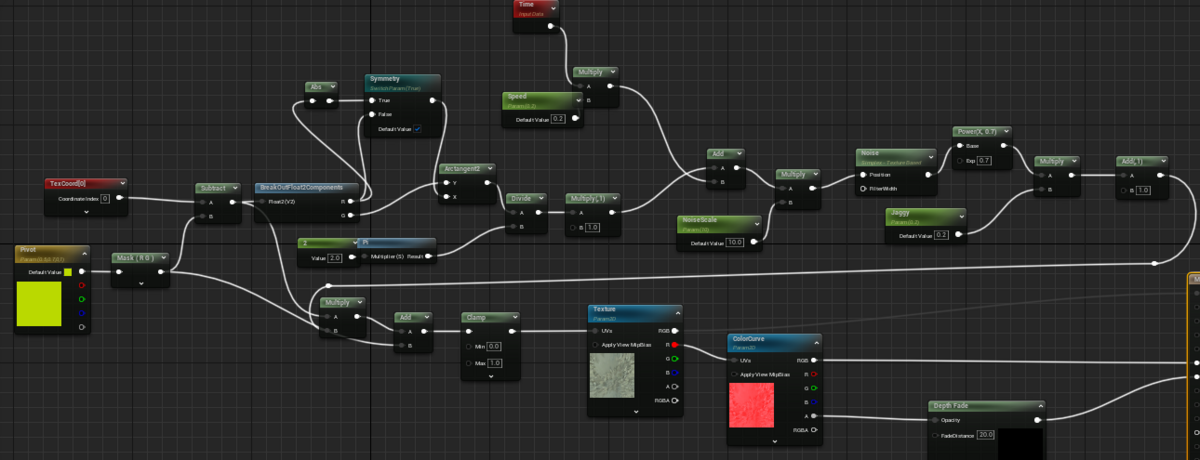
ワープ
望んだ形を得るには技術が必要かもしれません。
下の例では濃度マップの参照位置を放射状のノイズでずらしています。
ワープ量を与えるようなテクスチャを補助的に用いるのもよさそうです。
まとめ
感想や質問などがありましたらお寄せください。
Anime Aura VFX 技術解説②
UE5 向けの NiagaraSystem アセットである Anime Aura VFX についての技術解説です。 第１回 Anime Aura VFX の原理 今回はパーティクルの位置を用いて2次元の濃度マップを作製するプロセスについての説明です。 パーティクル以外のパーティクル Set では上から順に、 のようなものの初期状態を決めています。 このエミッターはパーティクルを一切発生させないため、ParticleSpawn / ParticleUpdate ではほぼ何もせずに SimulationStage の処理に入ります。 ScalarFieldGrid のうち、現フレームの情報を書き込む部分を 0 クリアします。 Grid2D について DrawArray / DrawBones / DrawParticle の作用は殆ど同じで、 以下が NM Bones to Scalar Field モジュールのグラフです。 長いコードではありませんが変数の命名がけっこう適当かつコメントが無いので読みづらいかもしれません。 繰り返しになりますが、ScalarFieldGrid の１ピクセル（仮）につき一度このコードが実行されます。 以下に概念図を載せます。 上記の処理で作成されたマップを、「流れ」を加えつつ直前のマップと合成します。 処理の内容を図で表すと以下のような感じです。 Grid2D はテクスチャではないのでそのままではマテリアルに渡せません。 NiagaraSystem を用いてパーティクル（+SkeletalMesh）から2次元のテクスチャ（濃度マップ）を生成するプロセスについて説明しました。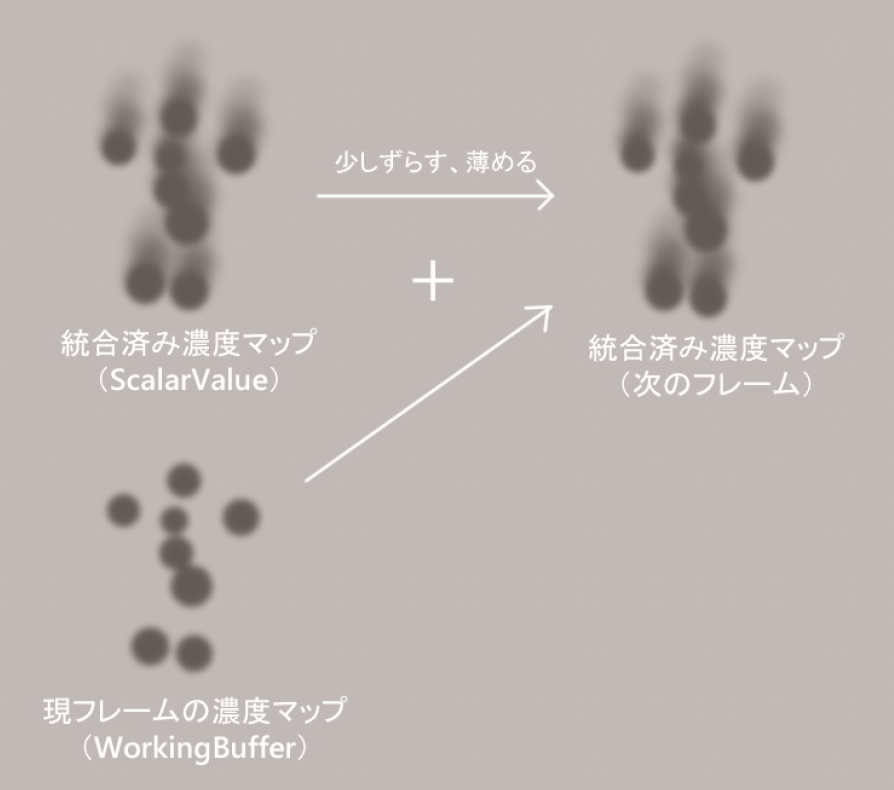
概要 この記事について
全３回に分けての解説を予定しています（これはボリューム等を見て変更する可能性があります）。
第２回 パーティクルの投影（本記事）
第３回 濃度マップ→表現
以下の知識を必要とする部分があります。読み進める中で詰まる場合は適宜ほかの資料で補うなどしてください。
Aura VFX NiagaraSystem 全体図
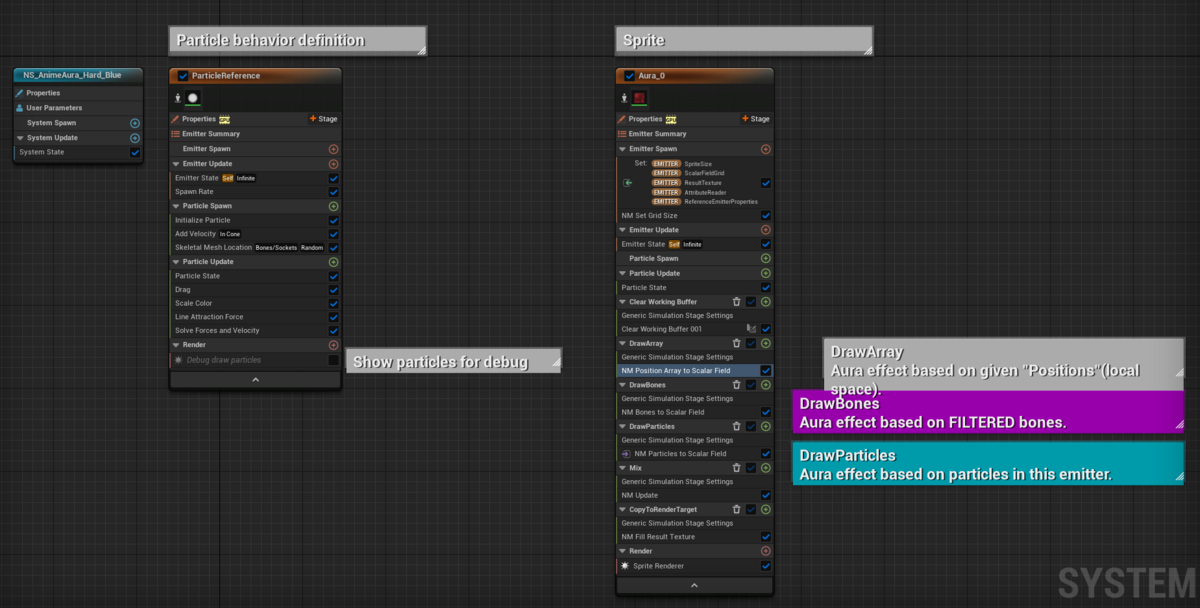
Anime Aura VFX には多くの NiagaraSystem が含まれますが、殆ど全てについて構造は共通しています。
左側の Emitter がパーティクル発生、右側が投影とスプライト表示を担います。パーティクルを発生させる
こちらはごく一般的な Emitter とあまり変わりません。
パーティクルを直接表示しないため、Renderer が無効になっています（有効化するとパーティクルの振る舞いを確認できます）。
キャラクターにまとわせるエフェクトですので、発生位置に SkeletalMeshLocation を用いています。
ここでパーティクルの発生量や位置・速度を制御することでオーラの挙動を変えることができます。
このシステムはGPUでの処理がやや複雑なものですので、パーティクルの数を極力抑えたいのが実情です。
投影処理においては上記のエミッターで発生させたパーティクルの他に、
SkeletalMesh のボーンの位置を「大きいパーティクル」のように扱います。
ボーン由来のパーティクルでオーラの概形を決め、実際のパーティクルで「揺らぎ」を作るような形をとっています。パーティクルの位置を投影する
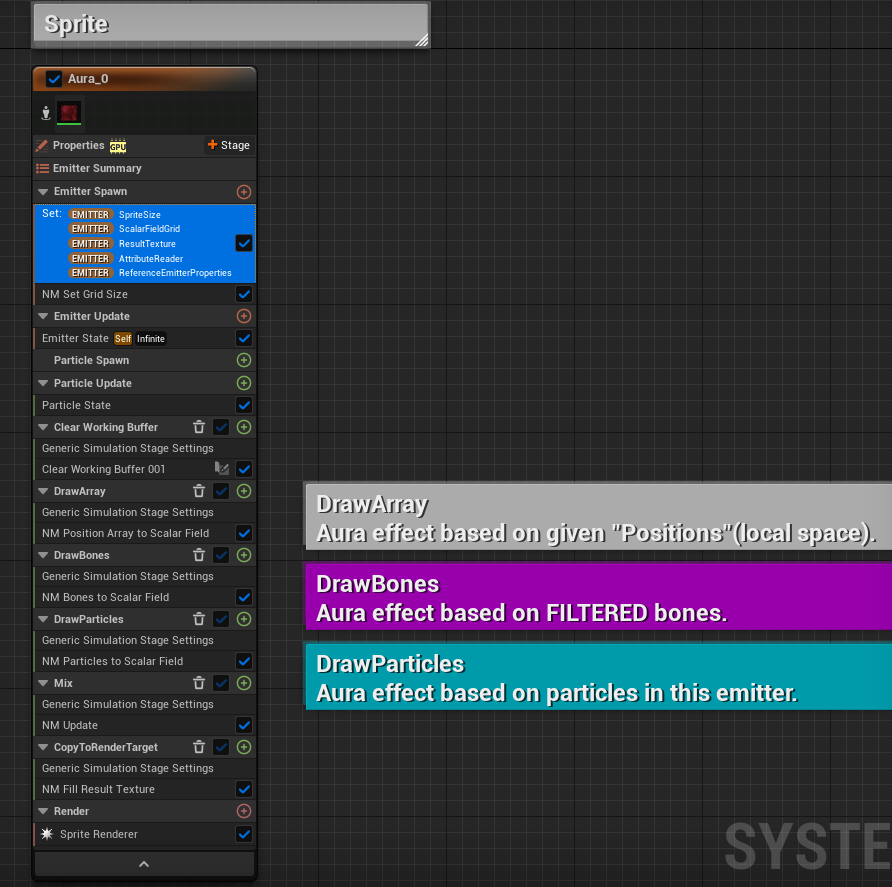
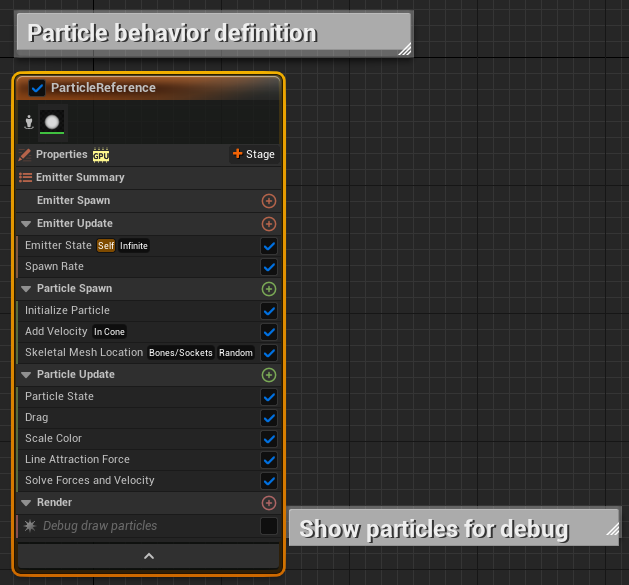
右側です。本システムの特徴からすると、こちらのエミッターが本体と言えるでしょう。
エミッター（放出するもの）と言いながらパーティクルを一切生成しないのが少し変わったところです。
コメントを付けている部分（DrawArray/DrawBones/DrawParticles）が実際に投影を行っている部分ですが、初期化から順を追って説明していきます。Emitter Spawn
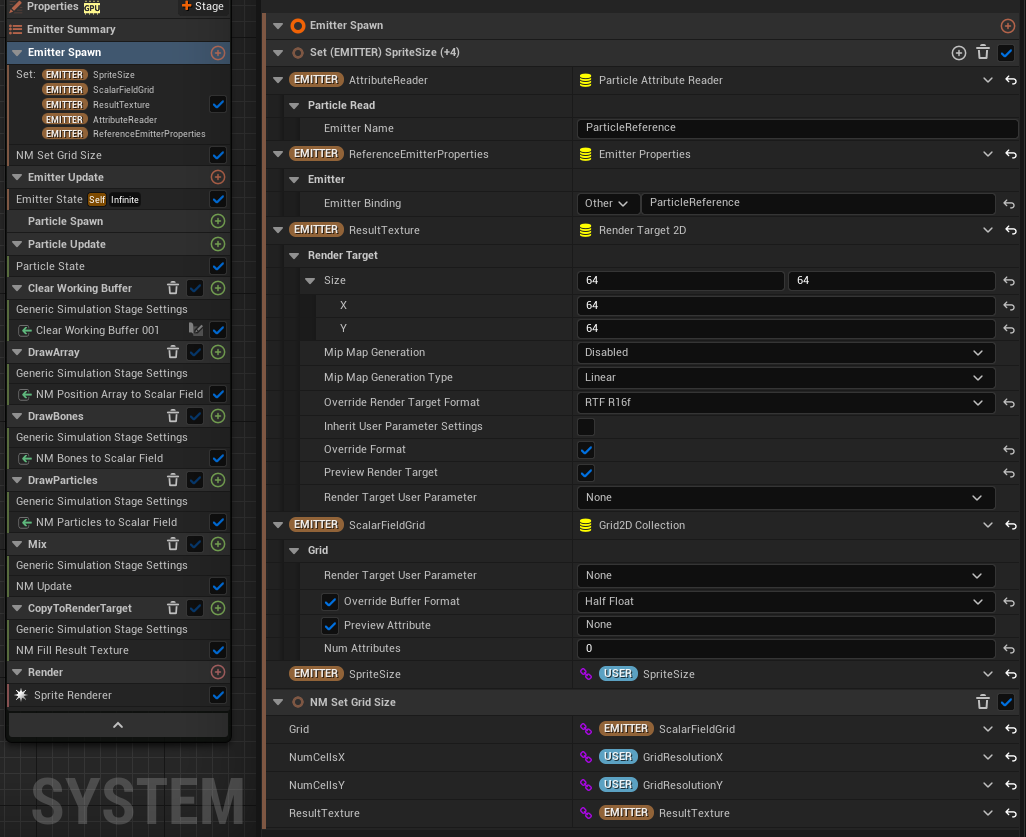
エミッター内で使用するパラメータはここで初期化されます。
さいごに、NM Set Grid Size では ScalarFieldGrid のサイズを決定します。投影処理
上から順に説明していきます。
Clear Working Buffer
ここで ScalarFieldGrid（Grid2D）について触れておきます。
ScalarFieldGrid は Grid2D という型を持ちますが、これは2次元配列状の構造を持ったデータです。
「ピクセルのフォーマットを自由に設定できるテクスチャ」のように考えればイメージとしては大体合っている気がします。
実際、NiagaraEditor の中では Grid2D の値をテクスチャのような感じでプレビューが可能です。
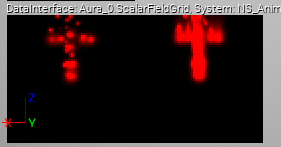プレビューの様子。
ScalarFieldGrid には
* 1フレーム分のデータを書き込む WorkingBuffer
* フレームを跨いで WorkingBuffer を合成して得る ScalarValue
という二つのスカラー値を保存していますので、二枚の画像を並べたように表示されます。DrawXXX
元となる（仮想的な）パーティクルの位置情報がそれぞれ 「決められたベクトル配列（多分あまり使わない）」「SkeletalMesh から得るボーン位置」「パーティクルの位置」 という違いがあるくらいです。
これらは、パーティクルの位置をスプライトの平面上へ投影して ScalarFieldGrid への書き込みを行います。
ここでは DrawBones を取り上げて説明します。準備
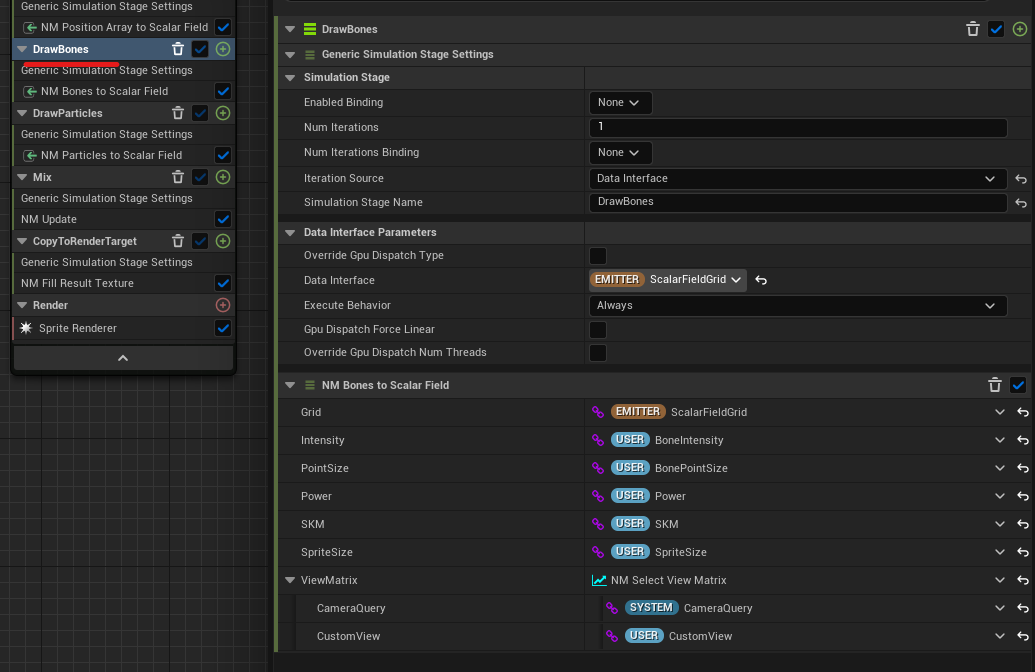
グラフに入る前にモジュールの設定です。
Niagara SimulationStage では「何らかのデータ集合に対して繰り返し処理を行う」ことができます。
何らかのデータ集合とはパーティクルであったりそれ以外（テクスチャ や Grid2D）であったりします。
画像中の Iteration Source に「何について繰り返すか」を指定します。
ここでは Iteration Source として ScalarFieldGrid （Grid2D）を用います。
そうすると、モジュールのグラフ（から生成されるシェーダーコード）が ScalarFieldGrid の各要素（ピクセル的なもの）に対して実行されることになります。計算
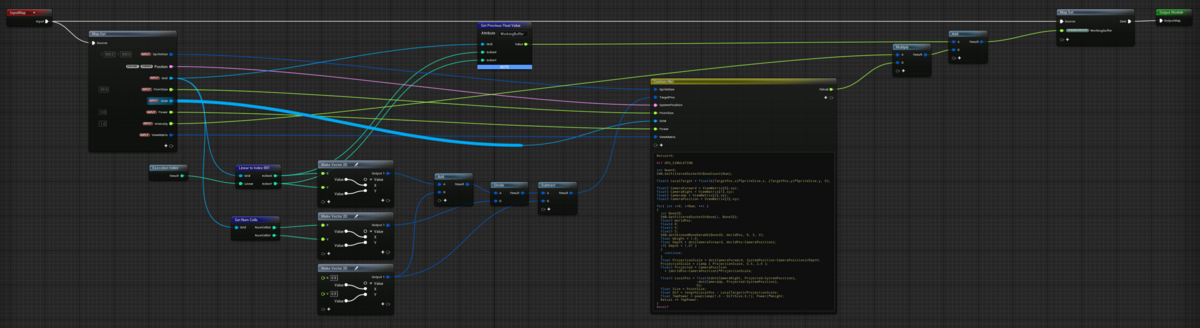
Niagara Module においてはわりとよくあることかと思いますが、主要な計算はHLSL コードの部分で行われます。
以下がその部分を拡大したものです。
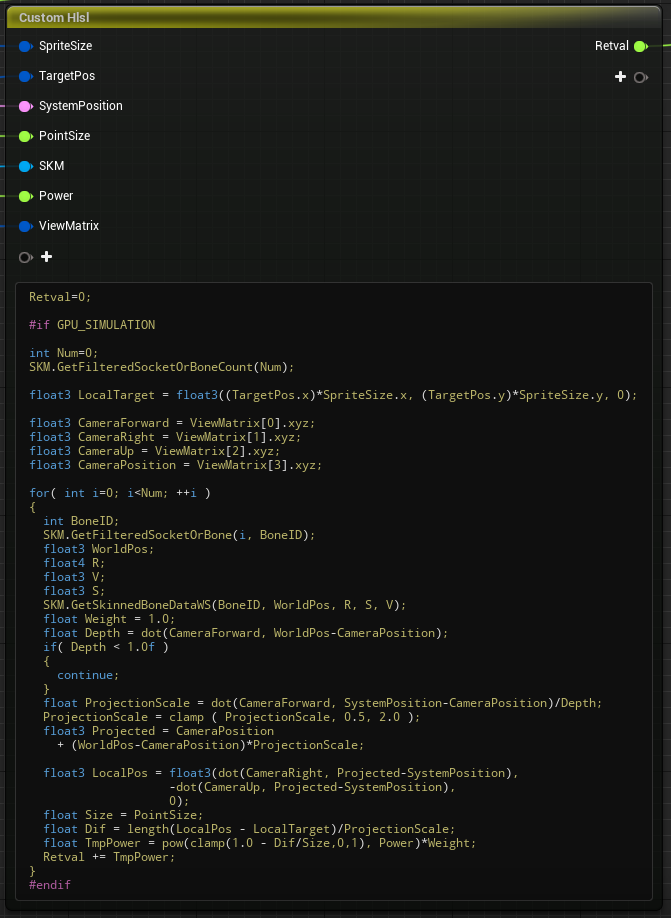
ですので補助線として変数の意味を幾つか書いておきます：
Num：パーティクル数
LocalTarget：ピクセル（仮）のローカル座標（スプライト中心を基準とした平面上の座標）
Projected：スプライト上に投影された座標（ワールド）
LocalPos：それをローカルに変換したもの
TmpPower：そのパーティクルにより生じる"濃度"
内容としては、全てのパーティクル（ここではボーンですが）についてスプライト平面への投影を行いピクセル（仮）との距離から濃度を算出して足し込んでゆくようになっています。
遠近法も適用され、カメラの近いパーティクルほど大きく描かれることになります。
0/1 ではなく、パーティクルが投影される位置がピクセル（仮）に近いほど濃く塗るようにしてグラデーションを作ります。
いわゆる2Dメタボールと同じような考え方ですので、このワードで検索してみると理解が捗るかもしれません。
このようにして、下の画像の左側のようなマップが作成されます。
Mix
画像左のマップを少しずつずらしつつ薄めながら足していくことを繰り返して右のマップを得ます。
CopyToRenderTarget
ここで ScalarFieldGrid から、統合後のマップを RenderTarget へコピーします。
右下がコピー元（統合されたマップ）、左上が結果の RenderTarget です。
もののついでに周辺部をフェードアウトさせる処理を行っています。まとめ
Anime Aura VFX には色々な見た目のエフェクトが含まれていますが実はここまでの部分は殆ど共通しており、多少パラメータが異なるくらいです。
出来上がった濃度マップを用いてどのように処理するかによって様々な外観を作り出すことが可能となっています。
次回はそちらについて解説する予定です。
Anime Aura VFX 技術解説①
UE5 向けの NiagaraSystem アセットである Anime Aura VFX についての技術解説です。 第１回 Anime Aura VFX の原理（本記事） このシリーズを通して以下のような知見を得られる可能性があります 第二回は NiagaraSystem、第三回は Material について多く触れることになる予定です。 実は以前すでにに軽い説明を書いているのですが、これをより具体的にしていく感じになります。 https://www.unrealengine.com/marketplace/en-US/product/a4e3c75346a74e85a7b0aa7505f23bb2www.unrealengine.com この手の表現が必要となった際にゲーム用エフェクトに馴染みのある方がひとまず思いつくのは以下の二つでしょうか。 前者は UE5 であれば NiagaraSystem を用いることになります。 Anime Aura VFX ではこれらのハイブリッド的な方法をとっています。 という手順となります。 Anime Aura VFX 及びそのメカニズムのさわりについて説明しました。
概要 この記事について
全３回に分けての解説を予定しています（これはボリューム等を見て変更する可能性があります）。
第２回 パーティクルの投影
第３回 濃度マップ→表現
よければ予習にどうぞ（これを読んでいる前提の記事にはしませんのでそこはご安心下さい）。
nkdtr.hatenablog.comAnime Aura VFX について
キャラクターの体から発する「気」「オーラ」「呪力」のようなものを表現することを主目的としたものです。
以下のような特徴を併せ持ちます。
大雑把な原理
一般的な手法で実現できないのかという問題
体表やボーン等からパーティクルを発生させることは容易いですし、実際ゲームではこの種の方法をとる場合が殆どでしょう。
ただ、2D的な表現は難しいかもしれません。
後者はフリップブック状のテクスチャやマテリアル芸を用いるアプローチです。
こちらはキャラクターのポーズにフィットさせる部分で難を抱えます。
大きく表示するなどポーズに依存しない表現に落とすことが多いでしょうか。
SceneCaptureを使うなどしてポーズを参照することも考えられますが処理負荷は高そうです。ハイブリッドな手法
つまり、
→そのパーティクルを2次元に投影、分布を「濃度マップ」に記録する
それぞれについての具体的な解説を次回以降で行います。まとめ
次回は NiagaraSystem (SimulationStage) でのパーティクルの投影についてです。
最も重要な部分であり長くなる見込みですので前後編に分かれる可能性があります。
Crystal Renderer 技術解説 補講
概要 この記事について
UE5 向けのプラグインである Crystal Renderer についての技術解説です。
全３回＋αに分けての解説を予定しています（これはボリューム等を見て変更する可能性があります）。
第１回：Crystal Renderer の原理
第２回：光の反射と屈折
第３回：形状をマテリアルに取り込む
補講：色収差について (本記事)
本記事は補講です。先に前回までの記事を読んで頂くことをお勧めします。
とりあえずどういうものか
まずは、どのような効果のものであるかを画像で示します。
順に 効果なし/あり のスクリーンショットです。
ふわっとした表現をすれば「色がついた感じ」になります。
いわゆる色収差について
基本的に、色収差というとレンズで像を作る際に色が分解される現象を指します
（Wikipediaの記事 へのリンクを貼っておきます）。
第２回で少し触れた屈折率についてですが、この値は光の波長により多少異なります。
多くの場合()において光はたくさんの波長を含みますので、レンズ等を通る際には波長ごとに軌道が異なるということになります。
（余談ですが、これに対して同一の波長のみを選択的に増幅させたものがみんな大好きレーザーです）
波長により像を結ぶ点がずれるために視覚的には色がぶれたように映るわけですね。
Crystal Renderer の"色収差"
レンズに限らず一般に光が屈折する際には光が波長毎に分解される現象が起こり、これは分光と呼ばれます。
虹に色が付くことや、ダイヤモンドのような無色の宝石が白い光の下でも色づいて見えることがあるのはこの現象によるものです。
（そういうわけで Crystal Renderer のそれを色収差と呼ぶのは正しくありませんが、エフェクトの名前としては分かりやすいので Aberration と称しています。 ）
原理としてはこのようなものですが、残念ながら忠実な色収差を再現するのは現実的ではありません。
現実的な光源は無数の波長成分を含んでいます（この分布を光源スペクトルといいます）。
そして波長毎に異なる軌道をとるわけですから、これを忠実に計算しようとすると計算量が膨大になります。
また、（少なくともゲームにおいて）CGの光源はスペクトルを情報として持ちません。
そういうわけなので、Crystal Renderer においては適当に波長が「長い」「中くらい」「短い」３つの軌道を計算して RGB 成分として合成しています。
まとめ
Crystal Renderer における Aberration (色収差っぽいエフェクト）について解説しました。
ナンバリングせず補講としたのはあまり本質的な部分ではないのと、他と比べてちょっといいかげんな内容だからです。
というわけで、一旦 Crystal Renderer に関する解説シリーズを終わります。
そういえば、UnrealEngine のポストプロセスにも色収差がありますがどのような実装になっているか調べてみるのも面白いかもしれません（他人任せ）。
Crystal Renderer 技術解説③
概要 この記事について
UE5 向けのプラグインである Crystal Renderer についての技術解説です。
全３回＋αに分けての解説を予定しています（これはボリューム等を見て変更する可能性があります）。
第１回：Crystal Renderer の原理
第２回：光の反射と屈折
第３回：形状をマテリアルに取り込む（本記事）
補講：色収差について
本記事は第３回です。先に前回までの記事を読んで頂くことをお勧めします。
前置き
前回、レイが平面（無限平面）に衝突したときの計算について解説しました。
しかし、「衝突させるまで」の部分についてが問題として残っています。
視点から発射されたレイが結晶表面に衝突する位置については、ピクセルシェーダーにデフォルトで渡されていますので問題ありません（UE5 の場合は WorldPosition としてマテリアル内でアクセスが可能）。
しかしそこから先、結晶内部を進むレイがどの位置で物体の表面に到達するかを知るには、形状のデータが不可欠です。
マテリアルを扱う方ならお分かりかと思いますが、ここでメッシュ自体を参照するわけにはいかないという点が問題になります。
形状データの表現
結論から提示しますが、形状はテクスチャとして表現されます。
例えばブリリアント・カット（いわゆるダイヤモンドの形状）のメッシュは Crystal Renderer のマテリアル内では以下のようなテクスチャになっています。
勘の良い人であれば何が行われているかを想像できるでしょうか。
今回はこれについての話です。
形状をマテリアルに取り込むにあたって、以下二点の状況・性質を利用します。
- 宝石の形状は多くの場合において凸多面体である（正確には曲面を含む場合でも、ポリゴンでは多面体で近似される）
- 凸多面体は平面の集合として記述できる
宝石の形状は多くの場合凸多面体である
字面の通りではありますが、凸多面体とは凹みのない多面体のことです。
宝石のカットという工程を動画などで見ると分かると思いますが（検索例）、
平坦なやすりで表面を削る操作によって面を作り出すことを繰り返すのが基本的な操作です。
この操作で凹みが発生することはありませんので、宝石の形状は多くが凸型になります（例外はあります）。
また、ブリリアントカットの周辺部分（ガードルと呼ばれます）など実物の宝石には曲面も存在することがありますが、
ゲーム用のCGにおいては多面体（ポリゴン）に落とし込まれるため曲面ではなくなります。
凸多面体は平面の集合として記述できる
「平面で削り取る」操作を繰り返して作られた形状は、削り取った平面の集合によって充分に表現できるはずです。
「同じ組み合わせの平面で削れば同じ形状になる」と表現すればより納得しやすいでしょうか。
前回の記事で少し触れたように、境界のない無限平面は四次元ベクトルで記述できます。
四次元ベクトルはRGBAカラーに変換できますので、一面あたり１ピクセルのテクスチャとして平面の集合を表現できることになります。
注意点として、ベクトルの成分は負の数や程度大きい数を含むことになります。
したがってそれを許容するようなフォーマットを用いるか、何らかの正規化によって０．０～１．０の範囲内に値が収まるようにする必要があります。
Crystal Renderer では RGBA16F（16ビット浮動小数）フォーマットのテクスチャを用いています。
メッシュを読み取って得た三角形の集合を平面の集合に直し、以下のような関数によってテクスチャ化しています。
UTexture2D *UCrystalRendererBPLibrary::CreateConvexMeshFromSurfaces(TArray<FVector4> &Surfaces, int &PlaneNum, int &TextureSizeW, UObject *TextureOwner) { if (Surfaces.Num() <= 0) { UE_LOG(LogTemp, Error, TEXT("Invalid surface list")); return nullptr; } // merge surfaces with (apploximately) same plane { TArray<int> RemoveList; for (int BaseIndex = 0; BaseIndex < Surfaces.Num() - 1; ++BaseIndex) { for (int AnotherIndex = BaseIndex + 1; AnotherIndex < Surfaces.Num(); ++AnotherIndex) { if (Surfaces[BaseIndex].Equals(Surfaces[AnotherIndex], 0.01f)) { RemoveList.AddUnique(AnotherIndex); } } } RemoveList.Sort(); for (int i = RemoveList.Num() - 1; i >= 0; --i) { Surfaces.RemoveAt(RemoveList[i]); } PlaneNum = Surfaces.Num(); } // decide texture size { int Width = 4; while (Width*Width < PlaneNum) { Width *= 2; } TextureSizeW = Width; } UTexture2D* Retval = CreateTexture(TextureOwner, TextureSizeW); TArray<FFloat16Color> Pixels; Pixels.SetNum(TextureSizeW*TextureSizeW); for (int i = 0; i < Surfaces.Num(); ++i) { Pixels[i] = FLinearColor(Surfaces[i]); } void *BulkData = Retval->GetPlatformData()->Mips[0].BulkData.Lock(LOCK_READ_WRITE); FMemory::Memcpy(BulkData, Pixels.GetData(), sizeof(FFloat16Color)*PlaneNum); Retval->GetPlatformData()->Mips[0].BulkData.Unlock(); #if WITH_EDITORONLY_DATA Retval->Source.Init(TextureSizeW, TextureSizeW, 1, 1, ETextureSourceFormat::TSF_RGBA16F, (const uint8*)Pixels.GetData()); #endif Retval->UpdateResource(); #if WITH_EDITOR Retval->PostEditChange(); #endif Retval->MarkPackageDirty(); return Retval; }
多角形の面は同一平面上のトライアングルを含みますので、これを除外する処理をついでに行っています。
これは衝突検出時の無駄な繰り返しを減らし、シェーダーの実行速度を有意に向上させる効果があります
（もちろん形状によりますが、宝石の面には四角形がけっこう多いためそれなりの効果が期待できます）。
形状データと衝突検出
さて、平面の集合として表現された形状とレイとの衝突をどのように計算すればよいでしょうか。
ふつうのポリゴンの場合は三角形とレイとの衝突判定を繰り返すことになりますが、
四次元ベクトルで表される（無限）平面の集合は頂点やエッジの情報を持ちません。
計算によりそれらを得ることも理屈上は可能でしょうが、死ぬほど効率が悪いということは想像に難くありません。
さいわい、これに関しては頓智めいた方法が存在します。
レイが形状の内部より開始するという条件が付くものの、各平面とレイとの衝突のうちもっとも早いものを採用するだけで凸多面体自体とレイとの衝突を求めることができます。
次の図を見ればこのことが直観的に分かるかと思います（もちろん実際には三次元空間を扱いますが、理屈は同じことです）。
（茶色い線が実際の形状データ、黒い線が元の形状、白い線がレイ、青グレーの丸がレイと平面との交点、黄色い丸がレイと多面体との交点を表します）
まとめ
レイの軌跡を計算するために形状をマテリアルに取り込む方法、及び取り込んだ形状の利用方法について説明しました。
なかなかに都合の良い話なのですが、凸多面体という条件下においてはこのような計算が成り立ちます。
Crystal Renderer の核となる理論についてはこれでおしまいです。
次は補講と称して色収差オプションについて少し書きます。
（おまけ）凸型でない形状
その場合においては軌跡の計算が正確ではなくなるため、ストアでの説明上は「凸型形状のメッシュに結晶風のマテリアルを適用するもの」としてあります。
正確でない計算の結果どうなるかと言えば、例えば結晶内部に透明な境界があるように見えたりします。
劇的に色が変わるわけではないので遠目にて気になる可能性は低いと思われますが、よく観察すれば違和感に気付くでしょう。
Crystal Renderer 技術解説②
UE5 向けのプラグインである Crystal Renderer についての技術解説です。 第１回：Crystal Renderer の原理 本記事は第２回です。先に前回の記事を読んで頂くことをお勧めします。 光の反射と屈折を計算するときに、レイおよび平面という二つの概念を扱いますのでこれについて確認しておく必要があります。 レイとは仮想的な光線であり、「開始点の座標」及び「進行方向のベクトル」を情報として持ちます ここで言う平面とは無限に続く平面を指します。 光が平面上で反射するときの経路について考えます。 屈折についてはもう少し複雑な計算になります。 この割合は光の当たる角度（入射角）によって異なります。 反射するのがこの割合で、残りは屈折すると考えます。 結晶内部で反射した光は別の位置で表面に到達し、ふたたび反射・屈折が起こります。 この結果を参照し、最後に環境マップからサンプリングした色の加重平均によって表示色を算出します。 反射および屈折の計算方法について説明しました。
概要 この記事について
全３回＋αに分けての解説を予定しています（これはボリューム等を見て変更する可能性があります）。
第２回：光の反射と屈折（本記事）
第３回：形状をマテリアルに取り込む
補講：色収差について
今回は物理（光）と数学（ベクトル）の話がメインです。基本情報
説明不要という方はこの部分を飛ばして下さい。レイについて
（プログラミング的にはこれを構造体としても良いですが、片方しか必要としない計算も多いため Crystal Renderer ではバラして扱っています）。
レイは「何かが直進したときにどこにぶつかるのか」を調べる際に頻繁に使われる概念ですのでご存知の方も多いでしょう。
ゲーム開発の場面においてはレイキャストという熟語で触れることが多いかもしれません。
検索すればどういうものかは分かると思いますので、ここでの説明は割愛します。平面について
平面は「法線ベクトル」および「平面上の座標と法線ベクトルとの内積（スカラー値）」で表されますので、プログラム上は四次元ベクトルに格納することができます。
このあたりで何を言ってるか分からないという方は次の記事などを読むとよいかもしれません。
ゲーム作りとかCGとかに関わる数学(初歩)① #数学 - Qiita
UE5 においては平面を表現するために FPlane（中身は TPlane）が定義されていますが、コンストラクタ等からお察しできるようにデータの内容としてはやはり四次元ベクトルと同等です。
光の反射と屈折
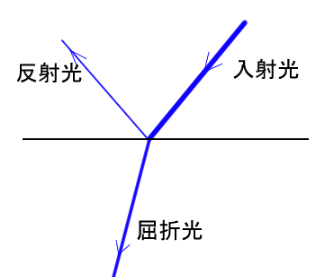
屈折率の異なる物質の境界に当たった光は一部が反射して戻り、一部が屈折して進入します。
Crystal Renderer では以下の関数でこれらの経路を計算しています（多少編集しつつ抜粋）。/**
* separate ray into refraction and reflection with weights
*/
void CollideRayWithPlane(float3 rayNormalized, float4 plane, float startSideRelativeRefraction, out float reflectionRate, out float3 reflection, out float3 refraction )
{
float3 rayVertical = dot(plane.xyz, rayNormalized) * plane.xyz;
reflection = rayNormalized - rayVertical*2.0;
float3 rayHorizontal = rayNormalized - rayVertical;
float3 refractHorizontal = rayHorizontal * startSideRelativeRefraction;
float horizontalElementSquared = dot(refractHorizontal, refractHorizontal);
float borderDot;
if( startSideRelativeRefraction > 1.0 )
{
borderDot = sqrt(1.0-1.0f/(startSideRelativeRefraction*startSideRelativeRefraction));
}
else
{
borderDot = 0.0;
}
// full reflection
if( horizontalElementSquared >= 1.0 )
{
reflectionRate = 1.0;
refraction = plane.xyz;
return;
}
float verticalSizeSquared = 1-horizontalElementSquared;
float3 refractVertical = rayVertical * sqrt( verticalSizeSquared / dot(rayVertical, rayVertical) );
float BaseReflection = pow((1.0-startSideRelativeRefraction)/(1.0+startSideRelativeRefraction), 2);
refraction = refractHorizontal + refractVertical;
reflectionRate = CalcReflectionRate(rayNormalized, plane.xyz, BaseReflection, borderDot);
return;
}
反射について
こういったことをプログラミングするときは、「まっすぐ跳ね返る」「鏡のように跳ね返る」といった漠然としたイメージではなく数学的な表現で考える必要があります。
この場合、反射後の進行方向は「元の進行方向ベクトルのうち、平面の法線方向成分のみが反転した向き」のように表現できます。
自信のない方は写経でも良いので一度ご自身でプログラミングしておくことをお勧めしますが、以下のように簡単なコードで計算できます（上のものからの抜粋）。
法線方向成分を抽出して二つ分引き算すれば反転するということですね。float3 rayVertical = dot(plane.xyz, rayNormalized) * plane.xyz;
reflection = rayNormalized - rayVertical*2.0;
屈折について
屈折時の進行方向についてはスネルの法則というものに従います。
スネルの法則 - Wikipedia
ようは、屈折前後の進行方向ベクトルについて平面に対して水平な成分の比が屈折率の比と反比例するということです。
進行方向ベクトルが正規化（長さを１にすること）されていれば、
①元の進行方向の水平成分に屈折率の比を乗算して屈折後の水平成分を算出
②長さが１となるよう垂直成分を補う
という手順で屈折後の進行方向を得ることができます。
上に示したコードから間引きながら関係する部分を抜粋したものを以下に示します。 float3 rayVertical = dot(plane.xyz, rayNormalized) * plane.xyz;
float3 rayHorizontal = rayNormalized - rayVertical;
float3 refractHorizontal = rayHorizontal * startSideRelativeRefraction; // 屈折後の水平成分
float horizontalElementSquared = dot(refractHorizontal, refractHorizontal);
float verticalSizeSquared = 1-horizontalElementSquared;
float3 refractVertical = rayVertical * sqrt( verticalSizeSquared / dot(rayVertical, rayVertical) ); // 屈折後の垂直成分
refraction = refractHorizontal + refractVertical;
反射と屈折との割合
基本的には浅い角度であるほど反射の割合が高くなることが知られています（俗にフレネル反射とか言われる効果です）。
また、屈折率の高い物質から低い物質への境界においては、入射角が一定以上の場合に「全反射」が起こります。
屈折率の高いダイヤモンドの中に複雑な反射が見えるのはこのことと関係があります。
反射の割合についてはフレネルの式というもので計算できます。
フレネルの式 - Wikipedia
実際の光には「波の振動方向」というものがあり、それに応じて反射率が異なるために複雑な式となります（ですので、水面やガラスで反射した光は偏光します）が、通常のコンピューターグラフィックスにおける光にそんなものはありませんので近似式を用います。
ページの下の方にあるコレ↓ですね。
この式にならい、Crystal Renderer では以下のような関数によって反射率を計算しています。float CalcReflectionRate(float3 normal, float3 ray, float baseReflection, float borderDot)
{
float normalizedDot = clamp( (abs(dot(normal,ray)) - borderDot) / ( 1.0 - borderDot ), 0.0, 1.0);
return baseReflection + (1.0-baseReflection)*pow(1.0-normalizedDot, 5);
}
反射・屈折を繰り返すことについて
これが繰り返されることによって複雑なパターンが表示されることになります。
理論上反射は無限に起こりますが、計算の都合上適当な回数で中断することになります。
当然ですが、この反射回数に応じて表示内容が変化します。
このように繰り返しが多いほど緻密な表示になりますが、１０→２０では劇的な変化がないことが見て取れるかと思います。
再帰的な処理になりますのでコードもそれに従いたいところですが、シェーダーコンパイラーがこれに対応していません（多分）ので通常のループとして記述することになります。
Crystal Renderer では以下のようなループになっています。
これまでの説明では意味の分からない部分を幾らか含んでいると思いますが、
反射・屈折を繰り返す光の経路をたどりながら計算し必要な情報を配列へと保存しています。 LOOP for( uint i = 0; i<MAX_REFLECTION; ++i )
{
if( i>= condition.MaxReflection )
{
break;
}
float hitTime=1000000.0;
float4 hitPlane=float4(1,0,0,1);
CheckCollideRayWithAllPlanes(tmpRayStart, tmpRayDirection, condition, hitPlane, hitTime);
hitTimes[i] = hitTime;
hitPlanes[i] = hitPlane;
if (hitTime < 0.0)
{
badRay = 1;
}
float3 rayEnd = tmpRayStart + tmpRayDirection*hitTime;
float reflectionRate;
float3 reflectionRay;
float3 refractionRay;
CollideRayWithPlane(tmpRayDirection, hitPlane, refractiveIndex, reflectionRate, reflectionRay, refractionRay);
reflectionRates[i] = reflectionRate;
refractionColors[i] = SampleEnvironment(refractionRay, condition);
depthColors[i] = float4(CalcColorCoefByDistance(hitTime, condition.MaterialColor),1);
tmpRayStart = tmpRayStart + tmpRayDirection * hitTime;
tmpRayDirection = reflectionRay;
}
まとめ
Crystal Renderer のシェーダーに関して全てではないものの、これが核心ではあります。
ただ、鋭い方はお気付きかもしれませんが、この計算を成立させるために重要な要素がまだ足りていません（冒頭にネタバレがありますが）。
それについてはまた次回をお待ちください。
